NCERT Solutions for Class 8 Maths CBSE
Understand all the chapters with the help of detailed NCERT solutions prepared for CBSE Class 8 Maths. The study material is developed by a skilled and experienced team of subject experts who specialise in simplifying the concepts for students. Class 8th Maths NCERT solutions have a detailed stepwise approach accompanied by conceptual insights and repetitive mention of formulae to ensure a solid base for the CBSE syllabus for Class 8 Maths.
CBSE Class 8 Maths solutions involves chapters like square and square roots, cube and cube roots, algebraic expressions, practical geometry, mensuration, factorisation, etc. that require developed logical and analytical skills. Students require rigorous practise to master every topic from the CBSE syllabus for Class 8 Maths. Having CBSE Class 8 Maths textbook solutions handy will accelerate the learning process. Refer to Class 8 Maths solutions to check your answers and understand ways to write stepwise solutions to problems from the CBSE syllabus for Class 8 Maths.
TopperLearning’s study material includes Class 8th Maths NCERT solutions and videos, CBSE sample papers Class 8, revision notes, most important questions, and subjective and objective questions. CBSE Class 8 syllabus notes are designed to be easily comprehensible so that students can refer to them at any hour. Updated CBSE guidelines have been followed by our academic team assuring complete success to the students. These CBSE Class 8 Maths notes help a student in scoring full marks in their examination. Class 8 Maths solutions ensure that a student adopts the right approach to study, even in the higher grades and numerous competitive exams.
Learn Class 8th Maths NCERT solutions with one of India’s leading educational brands and cash in your success in every exam. So kickstart your preparation and ace CBSE online Class 8 marking your path to success.
Chapter-wise list of ncert solution for Class 8 Maths
- Chapter 1 - Rational Numbers
- Chapter 2 - Linear Equations in One Variable
- Chapter 3 - Understanding Quadrilaterals
- Chapter 4 - Data Handling
- Chapter 5 - Squares and Square Roots
- Chapter 6 - Cubes and Cube Roots
- Chapter 7 - Comparing Quantities
- Chapter 8 - Algebraic Expressions and Identities
- Chapter 9 - Mensuration
- Chapter 10 - Exponents and Powers
- Chapter 11 - Direct and Indirect proportions
- Chapter 12 - Factorisation
- Chapter 13 - Introduction to Graphs
NCERT Solutions for CBSE Class 8 Mathematics
NCERT Solutions for CBSE Class 8 Mathematics Chapter 14
NCERT Solutions for CBSE Class 8 Mathematics Chapter 1 Rational Numbers
Practise NCERT Solutions for CBSE Class 8 Mathematics Chapter 1 Rational Numbers at TopperLearning. Learn to find the reciprocal of a given number by understanding the multiplicative inverse. Revise how a number can be placed on a number line and how problems based on the properties of rational numbers can be solved.
The numbers of the form 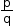 , where p and q are integers and q ≠ 0 are called rational numbers.
, where p and q are integers and q ≠ 0 are called rational numbers.
For example 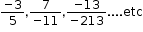 .
.
Rational numbers are
1. Closed under the operations of addition, subtraction and multiplication.
2. Commutative under the operations addition and multiplication.
3. Associative under the operations addition and multiplication.
The number
1. 0 is the additive identity for rational numbers.
2. 1 is the multiplicative identity for rational numbers.
The additive inverse of the rational number 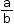 is
is 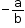 and vice-versa.
and vice-versa.
The reciprocal or multiplicative inverse of the rational number 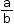 is
is 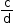 , if
, if 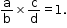 .
.
Multiplication is distributive over addition and subtraction of rational numbers. That is, for any three rational numbers a, b and c,
a ×(b + c) = a × b + a × c and a × (b - c) = a × b - a × c
Rational numbers can be represented on a number line. Between any two given rational numbers there are countless rational numbers.
Watch a quick problem-solving video.
This CBSE Class 8 Maths solutions covers rational numbers and basic problems related to rational numbers. Our subject experts have provided solutions to these problems. If you have doubts while practising the chapter solutions, post them on the ‘Ask a doubt’ section of our study portal. Our experts will respond through the platform and resolve your doubts at the earliest.
Chapter 1 - Rational Numbers Exercise Ex. 1.1
Use the correct properties and perform operations on rational numbers. Students are advised to follow correct steps and avoid calculation mistakes. Refer to NCERT Solutions for Class 8 Mathematics on TopperLearning, to check your answers once you have solved the exercise.
Chapter 1 - Rational Numbers Exercise Ex. 1.2
Represent the rational numbers on the number line and also find the rational numbers existing between two rational numbers. This exercise builds concepts related to the number system. Analyse your answers by referring to CBSE Class 8 Maths textbook solutions. Remember, our doubt solver "Ask a doubt" is there to solve your doubts round the clock.
NCERT Rational Numbers Class 8 Videos
NCERT Rational Numbers Class 8 Revision Notes
NCERT Rational Numbers Class 8 Most Important Questions
NCERT Rational Numbers Class 8 MCQ
NCERT Rational Numbers Class 8 Short Answer Questions
List of Sub chapters
Class 8 Maths- Introduction To Rational Numbers
Class 8 Maths - Representation On Number Line
Class 8 Maths - Rational Numbers Between Rational Numbers
NCERT Solutions for Class 8 Maths Chapter 2 Linear Equations in One Variable
Get the NCERT Solutions for CBSE Class 8 Maths Chapter 2 Linear Equations in One Variable on TopperLearning. Learn to solve equations with variables on both sides. Understand how to solve equations with numbers on one side or linear expressions on the other side.
- An equation is a statement of equality of two algebraic expressions involving one or more unknown quantities.
- An equation involving only a linear polynomial is called a linear equation.
For example: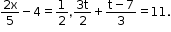
- Any value of the variable which makes the equation a true statement is called the solution or root of the equation.
For example: - 2 is root of the equation 3x - 2 = -8. - Any term of an equation may be taken to the other side with its sign changed, without affecting the equality. This process is called transposition.
- Without changing the equality, we may
i. add the same quantity to both sides of the equation.
ii. subtract the same quantity from both sides of the equation.
iii. multiply both sides of the equation by the same non-zero quantity.
iv. divide both sides of the equation by the same non-zero quantity. - If
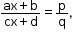 , then q (ax + b) = p (cx + d)
, then q (ax + b) = p (cx + d)
This process is called cross multiplication.
Also, practise linear equation problems based on real situations by using our Class 8th Maths NCERT solutions. If the chapter concepts are still giving you a hard time, check our practice tests. Use our ‘Ask a doubt’ section on our study platform to get guidance and solutions to difficult doubts
Chapter 2 - Linear Equations in One Variable Exercise Ex. 2.1
Solve basic operations on equations with one unknown variable. These questions also involve rational number calculations as solved in NCERT Solutions for CBSE Class 8 Maths. Such questions are often asked for 1-2 marks in the final examination. Refer to weekly tests and CBSE Class 8 Maths CBSE online Class 8 paper for practice.
Chapter 2 - Linear Equations in One Variable Exercise Ex. 2.2
Apply your knowledge of solving equations with one variable in a word problem. The step-wise approach for writing the solution can be understood properly with TopperLearning’s NCERT Solutions for Class 8 Maths.
Chapter 2 - Linear Equations in One Variable Exercise Ex. 2.3
Deal with variable on both sides in an equation and find the correct answer with NCERT Solutions for Class 8 Maths. Check each step of the solutions and practise some more problems using the most important questions and weekly test.
Chapter 2 - Linear Equations in One Variable Exercise Ex. 2.4
Apply your knowledge of solving a linear equation with a variable on both sides with NCERT Solutions for Class 8 Maths. Understand thoroughly what information is provided in the question and check each step of the calculation as given in our CBSE Class 8 Maths solution.
Chapter 2 - Linear Equations in One Variable Exercise Ex. 2.5
Simplify and solve the given linear equations with NCERT Solutions for Class 8 Maths. The knowledge of concepts such as LCM and operation on fractions, from the previous grades, are useful here. Revise these concepts from the revision notes provided by TopperLearning’s CBSE Class 8 notes.
Chapter 2 - Linear Equations in One Variable Exercise Ex. 2.6
A mixed bag of problems based on simplification and summary questions challenge students in this exercise. TopperLearning provides a well-explained and detailed solution with its NCERT Solutions for Class 8 Maths. Practise more problems with the weekly tests and CBSE Class 8 sample paper 2020-21.
NCERT Linear Equations in One Variable Class 8 Videos
NCERT Linear Equations in One Variable Class 8 Revision Notes
NCERT Linear Equations in One Variable Class 8 Most Important Questions
NCERT Linear Equations in One Variable Class 8 MCQ
NCERT Linear Equations in One Variable Class 8 Short Answer Questions
List Of Sub Chapters
Class 8 Maths- Solving Linear Equations
Class 8 Maths - Application Of Linear Equations
NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals
Refer to TopperLearning’s NCERT Solutions for CBSE Class 8 Mathematics Chapter 3 Understanding Quadrilaterals to revise your textbook problems. Understand the properties of quadrilaterals. Learn about convex quadrilaterals and concave quadrilaterals with step-wise answers for textbook questions.
Practise NCERT questions based on parallelograms and polygons with our CBSE Class 8 textbook solutions. Use them to explore the problem-solving techniques in Maths and learn to study independently. With self-study, you will have the confidence to solve problems on your own in your exam.
Chapter 3 - Understanding Quadrilaterals Exercise Ex. 3.1
Acquaint yourself with a special kind of polygon, Quadrilaterals, with NCERT Solutions for Class 8 Maths. Learn about their different properties about angles and sides. This exercise introduces and informs students about the basics of a quadrilateral.
- A plane figure formed by joining a number of points without lifting a pencil from the paper and without retracing any part of the figure is called a curve.
- A curve which does not cut itself is called an open curve.
- A curve which cuts itself is called a closed curve.
- A simple closed curve is a closed curve which does not pass through one point more than once.
- A simple closed curve made up of line segments is called a polygon.
- The line segments that constitute a polygon are known as its sides and their end points are known as the vertices of the polygon.
- Any two sides with a common end-point (vertex) are called the adjacent sides.
- The end points of the same side of a polygon are known as the adjacent vertices.
- The line segment obtained by joining vertices which are not adjacent are called the diagonals of the polygon.
- Number of diagonals in a polygon of n sides =
- A quadrilateral is a four sided polygon
- The sum of all the angles of a quadrilateral is 360o.
- If the line containing any side of the quadrilateral has the remaining vertices on the same side of it, then the quadrilateral is called a convex quadrilateral.
- In a convex quadrilateral the measure of each angle is less than 180o.
- The sum of the interior angles of a pentagon is 540o
Chapter 3 - Understanding Quadrilaterals Exercise Ex. 3.2
Apply the concept of Sum of the Measures of the Exterior Angles of a Polygon in this exercise with our NCERT Solutions for Class 8 Maths. These questions are popular in the objective category in CBSE Class 8 Maths.
Chapter 3 - Understanding Quadrilaterals Exercise Ex. 3.3
Dive in deeper to understand different kinds of quadrilaterals and their properties with some unusual problems. There are some more questions for assessment available along with revision notes, and weekly tests in CBSE Class 8 sample papers 2020-21. In addition, the NCERT Solutions for Class 8 Maths provide detailed solution for every question.
Chapter 3 - Understanding Quadrilaterals Exercise Ex. 3.4
Get to know more about rhombus, rectangle, and square in the final exercise of this chapter. Questions from this exercise have been asked in the subjective section of CBSE Class 8 sample paper 2020-21.
NCERT Understanding Quadrilaterals Class 8 Videos
NCERT Understanding Quadrilaterals Class 8 Revision Notes
NCERT Understanding Quadrilaterals Class 8 Most Important Questions
NCERT Understanding Quadrilaterals Class 8 MCQ
NCERT Understanding Quadrilaterals Class 8 Short Answer Questions
List Of Sub Chapters
Class 8 Maths- Polygons And Their Classification
Class 8 Maths - Quadrilaterals
Class 8 Maths - Properties Of Parallelograms
NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry
- A quadrilateral is a four-sided polygon.
- A quadrilateral has four sides, four angles and two diagonals, i.e., 10 elements. A quadrilateral can be constructed uniquely if at least five of its elements are given.
- A quadrilateral can be constructed uniquely, if we know any one of the following:
i. Four sides and one diagonal
ii. Four sides and one angle
iii. Two diagonals and three sides
iv. Two adjacent sides and three angles
v. Three sides and two included angles - For the construction of different type of quadrilaterals like parallelogram, rhombus, trapezium etc. we use their properties.
Chapter 4 - Practical Geometry Exercise Ex. 4.1
After learning about different quadrilaterals, apply the knowledge to construct quadrilaterals. NCERT Solutions for Class 8 Maths describe each and every step involved in constructing these quadrilaterals, along with rough diagrams. Refer to our videos and most important questions with TopperLearning’s CBSE online Class 8. Ask your doubts with our doubt solver “Ask a doubt”.
Chapter 4 - Practical Geometry Exercise Ex. 4.2
Questions from this exercise are asked for 3-4 marks hence make sure you go through NCERT Solutions for Class 8 Maths to understand the process and steps of geometrical constructions.
Chapter 4 - Practical Geometry Exercise Ex. 4.3
How to construct a quadrilateral when two adjacent sides and three angles are known? The solution to this query can be found on TopperLearning’s NCERT Solutions for CBSE Class 8 Maths.
Chapter 4 - Practical Geometry Exercise Ex. 4.4
Learn to construct quadrilaterals when three sides and two included angles are given, with our well-explained figures in NCERT Solutions for CBSE Class 8 Maths. Follow the steps of construction and refer to the video solutions to get more clarity.
Chapter 4 - Practical Geometry Exercise Ex. 4.5
The final exercise is all about some special cases for drawing quadrilaterals. Revise this concept better with our academic experts in CBSE Class 8 Maths textbook solutions.
NCERT Practical Geometry Class 8 Videos
NCERT Practical Geometry Class 8 Revision Notes
NCERT Practical Geometry Class 8 Most Important Questions
NCERT Practical Geometry Class 8 MCQ
NCERT Practical Geometry Class 8 Short Answer Questions
List Of Sub Chapters
Class 8 Maths- Construction Of Quadrilateral
Class 8 Maths - Construction Of Quadrilaterals Given Its Sides And Angles
Class 8 Maths - Construction Of Parallelograms
Class 8 Maths Construction Of Rhombus
Class 8 Maths - Construction Of Squares And Rectangles
NCERT Solutions for CBSE Class 8 Mathematics Chapter 5 Data Handling
Understand your Maths chapter concepts with TopperLearning’s NCERT Solutions for CBSE Class 8 Maths Chapter 5 Data Handling. Practise making a frequency distribution table or a bar graph according to the given data in your textbook exercises. Our solutions will guide you in making tables or graphs to represent data correctly using data handling techniques.
A collection of information is called the data. Data obtained in the original form is called a raw data.
The systematic arrangement of data, either in ascending or in descending order, is called an arrayed data.
The number of times a particular observation occurs is called its frequency.
The difference between the highest and lowest values of the observations in a given data is called its range.
When the number of observations is large, the data is usually organized into groups, called class intervals.
Pie chart represents data in relative quantities by using the area of sectors in the circle.
Central angle for a component = 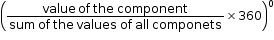
Check a video discussing about pie charts.
Chapter 5 - Data Handling Exercise Ex. 5.1
Grasp extensive knowledge about organising ungrouped data and also learn about bars that have a difference in this exercise. Tally your final answers with NCERT Solutions for CBSE Class 8 Maths and in case of doubt, get in touch instantly with our team of subject experts using the doubt solver “Ask a doubt”.
Chapter 5 - Data Handling Exercise Ex. 5.2
Learn more about deducing answers from pictorial representation and check your solutions with NCERT Solutions for CBSE Class 8 Maths.
Chapter 5 - Data Handling Exercise Ex. 5.3
NCERT Solutions for CBSE Class 8 Maths provides you with all the solutions to questions from this exercise, where probability and data have been combined to challenge students. This helps students with Maths in the higher grades and competitive exams as well.
NCERT Data Handling Class 8 Videos
NCERT Data Handling Class 8 Revision Notes
NCERT Data Handling Class 8 Most Important Questions
NCERT Data Handling Class 8 MCQ
NCERT Data Handling Class 8 Short Answer Questions
List Of Sub Chapters
Class 8 Maths- Frequency Distribution
Class 8 Maths - Bar Graphs And Histograms
NCERT Solutions for CBSE Class 8 Mathematics Chapter 6 Squares and Square Roots
Practise NCERT Solutions for CBSE Class 8 Maths Chapter 6 Squares and Square Roots with our experts to get better at Maths. Learn to factorise the given numbers. Revise the correct problem-solving methods to use square roots for finding answers to application questions.
Finding square roots through different methods
- Repeated subtraction
- We stated above that the square of a number is the sum of first n odd natural numbers. So, square root of a square number can be obtained by subtracting the successive odd natural numbers starting from 1 till we get 0.
- Prime factorization
- Express the number as the product of prime numbers, group the common primes in a pair, take one prime from each pair and then multiply to get the square root.
- Division method
- This method can also be used to find the square root of a non-perfect square or decimal number.
Watch a problem-solving video, below.
TopperLearning’s NCERT solutions will also guide you on how to make a number a perfect square by applying your CBSE Class 8 Maths syllabus concepts. For more practice, watch the video lessons, CBSE sample paper Class 8 and other self-learning materials available on our online education platform.
Chapter 6 - Squares and Square Roots Exercise Ex. 6.1
How do we find squares and square roots using patterns? Let us find it out with NCERT Solutions for CBSE Class 8 Maths.
Chapter 6 - Squares and Square Roots Exercise Ex. 6.2
Find squares observing some more patterns and Pythagorean triplets as we provide you with NCERT Solutions for CBSE Class 8 Maths. All your doubts will be solved by our Math experts on our doubt solver “Ask a doubt”.
Chapter 6 - Squares and Square Roots Exercise Ex. 6.3
Enlighten yourself with different methods of finding square roots in this exercise and check your answers with NCERT Solutions for CBSE Class 8 Maths.
Chapter 6 - Squares and Square Roots Exercise Ex. 6.4
Can we find square roots of numbers with decimal points? Have a problem with finding square roots? This topic can be best understood by watching our video solutions. Check your method and ask your queries on TopperLearning’s NCERT Solutions for CBSE Class 8 Maths. This chapter is all about calculations, hence it is advisable to take the weekly tests and refer CBSE Class 8 Maths sample papers for practice.
NCERT quares and Square Roots Class 8 Videos
NCERT quares and Square Roots Class 8 Revision Notes
NCERT quares and Square Roots Class 8 Most Important Questions
NCERT quares and Square Roots Class 8 MCQ
NCERT quares and Square Roots Class 8 Short Answer Questions
List Of Sub Chapters
Class 8 Maths- Properties Of Square Numbers
Class 8 Maths – Patterns In Square Numbers
Class 8 Maths - Square And Triangular Numbers
Class 8 Maths - Finding Square Root
Class 8 Maths - Estimating Square Roots
Class 8 Maths - Applications Of Squares And Square Roots
Class 8 Maths – Short Cut Methods For Finding Squares
NCERT Solutions for CBSE Class 8 Mathematics Chapter 7 Cubes and Cube Roots
Study Maths by using NCERT Solutions for CBSE Class 8 Maths Chapter 7 Cube and Cube Roots on our trusted study portal. Learn how factorisation can be used to solve problems on finding the perfect cube. Understand how to calculate cube roots as per the given data in your textbook questions of the CBSE Class 8 syllabus.
Cube number
Cube of a number is obtained when it is multiplied by itself thrice.
If ‘a’ is a number, then the cube of ‘a’ is a3 = a × a × a.
A natural number n is a perfect cube if n can be expressed as m3, for some natural number m. The numbers 1, 8, 27 are perfect cubes.
To find whether a number is a perfect cube or not:
Express the number as the product of prime factors.
If each factor appears three times in the prime factorization, the number is a perfect cube.
If there are one or more factor(s) which do not appear 3 (or multiples of 3) times, the number is a non-perfect cube.
64 = 4 × 4 × 4, is a perfect cube. 72 = 2 × 2 × 2 × 3 × 3 = 22 × 32, is not a perfect cube.
Watch a problem solving video, below to understand more on perfect cubes.
TopperLearning’s NCERT textbook solutions for CBSE Class 8 Maths will help you a great deal during chapter revision. If you feel stuck while trying to solve a particular question, visit our ‘Ask a doubt’ section to look for solutions or to post a question related to your doubt.
Chapter 7 - Cubes and Cube Roots Exercise Ex. 7.1
Solve this exercise and get introduced to cubes. The calculation part can be referred to from TopperLearning’s NCERT Solutions for CBSE Class 8 Maths.
Chapter 7 - Cubes and Cube Roots Exercise Ex. 7.2
Learning various methods of finding the cube root of a number and quickly tally your solutions with NCERT Solutions for CBSE Class 8 Maths. These questions are scoring, hence go through some practise questions from TopperLearning’s study material and CBSE Class 8 Maths sample papers.
NCERT Cubes and Cube Roots Class 8 Videos
NCERT Cubes and Cube Roots Class 8 Revision Notes
NCERT Cubes and Cube Roots Class 8 Most Important Questions
NCERT Cubes and Cube Roots Class 8 MCQ
NCERT Cubes and Cube Roots Class 8 Short Answer Questions
List Of Sub Chapters
NCERT Solutions for CBSE Class 8 Mathematics Chapter 8 Comparing Quantities
How to compare the speed of a scooter with that of a cycle? What steps should you follow to calculate the selling price of an article? Get your answers by revising textbook problems using NCERT Solutions for CBSE Class 8 Mathematics Chapter 8 Comparing Quantities.
Ratio and percentage
Ratio means comparing two quantities with each other.
Percentages are numerators of fractions with denominator 100. The symbol '%' is used for percent and it indicates multiplication with 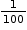
Increase or decrease percentage
Percentage increase/decrease = 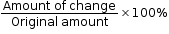
Watch a video that shown a problem-solving approach on the related concepts.
Discount
In order to give a boost to the sales of an item or to clear the old stock, articles are sold at reduced prices. This reduction is given on the Marked Price (MP) of the article and is known as discount.
Discount = MP – SP
Discount % = 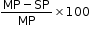
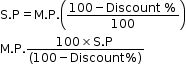
Simple Interest
If the interest is calculated uniformly on the original principal, it is called the simple interest.
If P, R, T stand for principal, rate and time respectively, and SI stands for simple interest, then
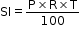
Understand the CBSE Class 8 Maths chapter concepts such as Principal, Cost Price, Rate of Interest, Marked Price etc. with our NCERT solutions. To score high marks in Maths, you need conceptual clarity and sufficient practice. Explore TopperLearning’s CBSE sample paper Class 8, online practice tests etc. to prepare well and to score high marks in your exam.
Chapter 8 - Comparing Quantities Exercise Ex. 8.1
Revise the concept of ratios and percentages by solving this exercise. Check CBSE Class 8 Maths Chapter 8 Exercise 8.1 Solution to compare your answers.
Chapter 8 - Comparing Quantities Exercise Ex. 8.2
You can familiarise yourself with CBSE Class 8 syllabus with the basic concept of computing increase and decrease in percentage and discounts. This exercise also focuses on understanding the real-life concept of Value added tax (VAT). An elaborate solution for every question of this exercise has been provided on TopperLearning’s NCERT Solutions for CBSE Class 8 Maths.
Chapter 8 - Comparing Quantities Exercise Ex. 8.3
Find how to calculate Compound Interest and also read how the formula for compound interest was deduced. Solve the exercise and check CBSE Class 8 Maths Chapter 8 Exercise 8.3 Solution to compare your answers.
Questions based on this concept are often asked in competitive exams, hence, students must refer to R D Sharma solutions for more practice questions.
NCERT Comparing Quantities Class 8 Videos
NCERT Comparing Quantities Class 8 Revision Notes
NCERT Comparing Quantities Class 8 Most Important Questions
NCERT Comparing Quantities Class 8 MCQ
NCERT Comparing Quantities Class 8 Short Answer Questions
List Of Sub Chapters
Class 8 Maths- Ratios Of Quantities
Class 8 Maths - Application Of Percentages
Class 8 Maths – Profit And Loss
Class 8 Maths – Compound Interest
NCERT Solutions for CBSE Class 8 Mathematics Chapter 9 Algebraic Expressions and Identities
Get the model answers by some of the best Maths experts to revise textbook problems. Check TopperLearning’s NCERT Solutions for CBSE Class 8 Maths Chapter 9 Algebraic Expressions and Identities. Learn to find the sum of algebraic expressions in your textbook problems. Also, practise multiplication, division, and subtraction of algebraic expressions with our Maths support resources.
What are constant and variable?
Constant is a symbol that takes fixed numerical value which is represented by letters.
Variable is a symbol that takes various numerical values which is represented by letters.
Algebraic Expression
A combination of constants and variables connected by the operators +, -, Χ and is known as an algebraic expression.
Example: 15 x 2 – 9x + 4xy is an algebraic expression.
What is an identity?
An identity is an equality, which is true for all values of variables in it.
On the other hand, an equation is true only for certain values of the variables in it. An equation is not an identity.
Some standard and important identities:
(a + b)2 = a2+2ab+b2
(a – b)2 = a2 – 2ab + b2
(a + b)(a – b) = a2 – b2
(x + a)(x + b) = x2 + (a + b)x + ab
Use of algebraic identities
The algebraic identities are useful in carrying out the square and products of algebraic expressions.
They can also be used as an alternative method to calculate product of numbers.
Watch a video to understand a problem solving approach based on the concepts of multiplication of polynomials
Revise the concept of identities and practise application of identities with our CBSE Class 8 Maths NCERT textbook solutions. All our Maths self-study resources are available online and can be used according to your revision schedule.
Chapter 9 - Algebraic Expressions and Identities Exercise Ex. 9.1
Study about Terms, Factors and Coefficients for Monomials, Binomials and Polynomials in an Algebraic expression. This exercise also has questions on the Addition and Subtraction of Algebraic Expressions. Attempt these questions and refer to the solution sheet on TopperLearning’s NCERT Solutions for CBSE Class 8 Maths. More the practice, better the understanding. Attempt questions from the weekly test and most important questions from this chapter.
Chapter 9 - Algebraic Expressions and Identities Exercise Ex. 9.2
After understanding the addition and subtraction of algebraic expressions, let us learn about the Multiplication of Algebraic Expressions and check our solutions by referring to TopperLearning’s NCERT Solutions for CBSE Class 8 Maths.
Chapter 9 - Algebraic Expressions and Identities Exercise Ex. 9.3
The multiplications process for Algebraic Expressions have many aspects and hence is divided into sections in CBSE Class 8 Maths. Understand the process of Multiplying a Monomial by a Polynomial with TopperLearning’s NCERT Solutions for CBSE Class 8 Maths. Solving ehese problems gives an eighth-grader confidence to solve more complex problems.
Chapter 9 - Algebraic Expressions and Identities Exercise Ex. 9.4
Let’s take a step ahead and grasp the process of multiplying a Polynomial by a Polynomial with TopperLearning’s NCERT Solutions for CBSE Class 8 Maths. Feel free to use our doubt solver “Ask a doubt” when you have doubts. Address your concerns by practicing more by using our video lectures, MCQs, and CBSE Class 8 Maths sample paper.
Chapter 9 - Algebraic Expressions and Identities Exercise Ex. 9.5
Learn basic identities that are applicable to every grade after class 8. These identities are extremely important in CBSE Class 8 syllabus and are very often asked in exams. Solve every question from the exercise and take the tests to evaluate your knowledge. Refer to CBSE Class 8 Maths sample papers for better insight.
NCERT Algebraic Expressions and Identities Class 8 Videos
NCERT Algebraic Expressions and Identities Class 8 Revision Notes
NCERT Algebraic Expressions and Identities Class 8 Most Important Questions
NCERT Algebraic Expressions and Identities Class 8 MCQ
NCERT Algebraic Expressions and Identities Class 8 Short Answer Questions
List Of Sub Chapters
Class 8 Maths- Introduction To Algebraic Expressions
Class 8 Maths – Addition And Subtraction Of Algebraic Expressions
Class 8 Maths - Multiplication Of Polynomials
Class 8 Maths - Algebraic Identities
Class 8 Maths – Expansion Using Algebraic Identities
NCERT Solutions for CBSE Class 8 Mathematics Chapter 10 Visualising Solid Shapes
Understanding Maths problems become simple when you can refer to accurate model answers aligned with the syllabus. Get these NCERT Solutions for CBSE Class 8 Mathematics Chapter 10 Visualising Solid Shapes online at TopperLearning. Understand how to visualise shapes from different angles such as front view, side view, and top view.
With our online CBSE Class 8 Maths NCERT solutions, you can revise 3D shapes and Euler’s formula as well. To further learn the visualisation of solid shapes, look at our online practice tests, concept videos, question papers, and more.
Chapter 10 - Visualising Solid Shapes Exercise Ex. 10.1
Analyse three-dimensional views of solid shapes and apply your understanding in this exercise. TopperLearning’s NCERT Solutions for CBSE Class 8 Maths will help you tally your solutions.
Chapter 10 - Visualising Solid Shapes Exercise Ex. 10.2
Learn more about the concept of space with TopperLearning’s NCERT Solutions for CBSE Class 8 Maths. Refer to the video lessons and CBSE Class 8 Maths sample papers to understand the types of questions asked in this category.
Chapter 10 - Visualising Solid Shapes Exercise Ex. 10.3
Learn about edges, sides, and vertices of different polygons and solid shapes in CBSE Class 8 Maths. The knowledge of these is required in higher grades. Refer to solutions with conceptual insight with TopperLearning’s CBSE Class 8 Maths textbook solutions.
NCERT Visualising Solid Shapes Class 8 Videos
NCERT Visualising Solid Shapes Class 8 Revision Notes
NCERT Visualising Solid Shapes Class 8 Most Important Questions
NCERT Visualising Solid Shapes Class 8 MCQ
NCERT Visualising Solid Shapes Class 8 Short Answer Questions
NCERT Solutions for CBSE Class 8 Mathematics Chapter 11 Mensuration
How to calculate the perimeter of a square or a rectangle? How to compute the area of a pentagon? Learn by practicing the NCERT Solutions for CBSE Class 8 Maths Chapter 11 Mensuration with TopperLearning. When you practise the expert solutions, you will understand the ways to apply the techniques to find the area of real objects.
Area of a polygon (or field) can be calculated by suitably dividing it into triangle, rectangle, trapezium etc. Surface area of a solid is the sum of the areas of all its faces. Amount of region occupied by a solid is called its volume.
For a cuboid of length l, breadth b and height h, we have:
Volume of cuboid = (l b h) cubic units
Total surface area of cuboid = (lb + bh + lh) sq units
Lateral surface area of cuboid = {2(l + b) h] sq units
Diagonal of cuboid = 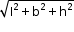 units
units
Unit conversion:
1 cm3 = 1 mL
1 L = 1000 cm3
1 m3 = 106 cm3 = 1000 L
Watch a problem-solving video based on perimeter of polygons.
With the CBSE Class 8 NCERT solutions for this Maths chapter, you can learn the way to find the surface area of cubes and cuboids too. For commonly asked chapter-specific questions and expert answers, visit the ‘Ask a doubt’ section on our study platform.
Chapter 11 - Mensuration Exercise Ex. 11.1
Compute the area of rectangular fields and find the correct answer with CBSE Class 8 Maths textbook solution. These questions are asked in the subjective section. Refer to TopperLearning’s CBSE Class 8 Maths sample papers for more insight.
Chapter 11 - Mensuration Exercise Ex. 11.2
Calculate the area of a trapezium and learn its application with TopperLearning’s CBSE Class 8 Maths textbook solutions. Use our doubt solver “Ask a doubt” if you have doubts. Clear your concerns by practising more using video lectures, MCQs, and TopperLearning’s CBSE Class 8 Maths sample papers.
Chapter 11 - Mensuration Exercise Ex. 11.3
Discover the process of computing the area of general quadrilateral polygons and special quadrilaterals accompanied by Surface Area of Cube, Cuboid and Cylinder with TopperLearning’s CBSE Class 8 Maths textbook solutions.
Chapter 11 - Mensuration Exercise Ex. 11.4
TopperLearning’s CBSE Class 8 Maths textbook solutions helps you with a step-wise solution for calculating the Volume of Cube, Cuboid and Cylinder. These questions are most important in terms of high order thinking skills.
NCERT Mensuration Class 8 Videos
NCERT Mensuration Class 8 Revision Notes
NCERT Mensuration Class 8 Most Important Questions
NCERT Mensuration Class 8 Short Answer Questions
List Of Sub Chapters
Class 8 Maths- Area And Perimeter Of Quadrilaterals
Class 8 Maths – Area Of Polygonal Regions
Class 8 Maths – Perimeter Of Polygons
Class 8 Maths – Surface Area: Cubes And Cuboids
Class 8 Maths – Volumes: Cubes And Cuboids
Class 8 Maths – Surface Area And Volume Of Cylinder
Class 8 Maths – Problems On Mensuration
NCERT Solutions for CBSE Class 8 Mathematics Chapter 12 Exponents and Powers
Enhance your Maths skills with the support of TopperLearning’s NCERT Solutions for CBSE Class 8 Mathematics Chapter 12 Exponents and Powers. Study Maths at your own pace with expert answers for all your Maths textbook exercises. TopperLearning gives you free access to all these expert answers online 24/7.
- Large numbers can be written in shorter form using exponents.
For example: 1000 = 103
Here, 103 is called the exponential form of 1000.
10the number that is being multiplied) is called the base.
3 (number of times the same number is multiplied by itself) is called the power (or index or exponent) - As the exponent increases by 1 the value becomes ten times the previous value.
- As the exponent decreases by 1 the value becomes
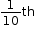 the previous value.
the previous value. - For any non-zero integer ‘a’,
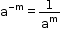 , where m is a natural number.
, where m is a natural number. - For a and b non-zero rational numbers, then
- Laws of exponents: If 'a' and 'b' are rational numbers different from zero and if x, y are positive integers, then
- ax ay = ax+y
- ax ay = ax – y
- (ax)y = axy
- (ab)x = ax bx
- a0 = 1
- (-1)odd number = -1
(-1) even number = 1
Watch a quick video on exponents.
Also, understand the laws of exponents and revise the problems based on powers with negative numbers. Our NCERT textbook solutions for CBSE Class 8 Maths have you covered. For complete self-study materials, you may also want to take a look at our video lessons, solved question papers, and more.
Chapter 12 - Exponents and Powers Exercise Ex. 12.1
Revise and apply the laws of exponents on the given questions and compare your answers with TopperLearning’s CBSE Class 8 Maths textbook solutions.
Chapter 12 - Exponents and Powers Exercise Ex. 12.2
Compare numbers with very high power with smaller numbers and simplify the solutions with TopperLearning’s CBSE Class 8 Maths solutions. Such questions are asked in the MCQ category. Hence, it is wise to refer to some TopperLearning’s extra MCQs and CBSE sample papers Class 8 for practice.
NCERT Exponents and Powers Class 8 Videos
NCERT Exponents and Powers Class 8 Revision Notes
NCERT Exponents and Powers Class 8 Most Important Questions
NCERT Exponents and Powers Class 8 MCQ
NCERT Exponents and Powers Class 8 Short Answer Questions
List Of Sub Chapters
Class 8 Maths- Exponent Notation
Class 8 Maths – Numbers In Standard Form
NCERT Solutions for CBSE Class 8 Mathematics Chapter 13 Direct and Inverse Proportions
Revise concepts from the syllabus using TopperLearning’s NCERT Solutions for CBSE Class 8 Mathematics Chapter 13 Direct and Indirect Proportions. Learn to apply the concept of direct proportion to find answers in real-life scenarios such as whether a pigment and its base are in the right proportion.
Two quantities x and y are said to be in direct proportion if whenever the value of x increases (or decreases), then the value of y increases (or decreases) in such a way that the ratio 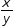 remains constant.
remains constant.
Example: Work done is directly proportional to the number of men working on it.
Two quantities x and y are said to be indirect proportion if whenever the value of x increases (or decreases), then the value of y decreases (or increases) in such a way that xy remains constant.
Example: The time taken by any vehicle in covering a certain distance is inversely proportional to the speed of the car.
Watch a problem solving video on indirect proportion.
Map is a miniature representation of a large regions. Hence we can say that scale of a map is based on the concept of direct variation.
Suppose A can finish a piece of work in n days. Then, work done by A in 1 day = 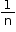
When a person A completes 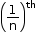 part of the work in one day, then A will take n days to complete the work.
part of the work in one day, then A will take n days to complete the work.
In a cistern there are two pipes. The inlet is the pipe that fills the cistern and the outlet is the pipe that empties the cistern.
When an inlet fills the cistern in ‘n’ hours, then it will fill up 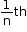 part of the cistern in one hour.
part of the cistern in one hour.
When an outlet empties the cistern in ‘n’ hours, then it will empty out 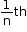 part of the cistern in one hour.
part of the cistern in one hour.
Multiplicative inverse of a number is called the reciprocal of a number.
With TopperLearning’s NCERT textbook solutions, learn how to solve Maths problems based on inverse proportion. To improve your Maths skills and to get a high score in your exam, use our CBSE Class 8 Maths videos, online mock tests, practice question papers etc.
Chapter 13 - Direct and Indirect proportions Exercise Ex. 13.1
Master the concept and application of Direct Proportion with TopperLearning’s elaborated study material comprising videos, MCQs, CBSE sample papers Class 8 and tests. Tally all your solutions with TopperLearning’s CBSE Class 8 Maths solutions.
Chapter 13 - Direct and Indirect proportions Exercise Ex. 13.2
CBSE Class 8 Maths textbook solution questions are asked in the subjective category for 3-4 marks. Hence, refer to TopperLearning’s extra questions and CBSE Class 8 sample papers 2020-21 for more practice.
NCERT Direct and Inverse Proportions Class 8 Videos
NCERT Direct and Inverse Proportions Class 8 Revision Notes
NCERT Direct and Inverse Proportions Class 8 Most Important Questions
NCERT Direct and Inverse Proportions Class 8 MCQ
NCERT Direct and Inverse Proportions Class 8 Short Answer Questions
List Of Sub Chapters
Class 8 Maths- Direct Proportion
Class 8 Maths – Inverse Proportion
NCERT Solutions for CBSE Class 8 Mathematics Chapter 14 Factorisation
Study Maths at your convenience with TopperLearning’s NCERT Solutions for CBSE Class 8 Maths Chapter 14 Factorisation. Revise the lessons on the division of algebraic expressions by going through our chapter solutions from CBSE Class 8 syllabus. Get over your fear of the concept of factorisation by practising numerous textbook solutions given by our subject experts.
- Factorisation of an expression means writing it as a product of its factors.
- An irreducible factor is a factor which cannot be expressed further as a product of factors.
- Factorisation using common factor method:
Step 1: Find the factors of the individual terms of the given expression.
Step 2: Find out all the common factors between the terms involved.
(same as finding HCF of terms)
Step 3: This common factor would be one factor of the given expression. Other factor would be the expression obtained on dividing the given expression by common factor. - Rearranging the given expression to a convenient form allows us to form groups leading to factorization. This is regrouping.
- Factorisation by regrouping terms
Step 1: Arrange the terms of the given expression in groups in such a way that all the groups have a common factor.
Step 2: Factorise each group.
Step 3: Take out the factor which is common to all such groups. - Factorisation using following identities:
i. a2 + b2 + 2ab = (a + b)2
ii. a2 + b2 - 2ab = (a - b)2
iii. a2 - b2 = (a + b)(a - b)
iv. x2 + (a + b)x + ab = (x + a)(x + b)
Method: Express the give expression as the LHS of the identities given above by choosing suitable values of a and b. Using identities, factorise the expression as RHS.
Watch this video on factorizing using identities.
Our study portal supports you during your exams with easy access to chapter-wise CBSE Class 8 Maths NCERT solutions any time of the day, any day of the week. So, revise your Maths chapters and be ready to excel in your exam.
Chapter 14 - Factorisation Exercise Ex. 14.1
Gain knowledge about yet another concept in CBSE Class 8 Maths that has vast applications in the higher grades. Solve problems and check your answers with TopperLearning’s CBSE Class 8 Maths textbook solutions on finding common factor and factorisation of a polynomial.
Chapter 14 - Factorisation Exercise Ex. 14.2
Factorise using identities and get the perfect solution with TopperLearning’s CBSE Class 8 Maths textbook solutions.
Chapter 14 - Factorisation Exercise Ex. 14.3
Earlier, we focused on the Multiplication of Algebraic expressions. Here, we shall look at the concept of Division of Algebraic Expressions with steps. TopperLearning’s CBSE Class 8 Maths solutions come in handy as they are detailed.
Chapter 14 - Factorisation Exercise Ex. 14.4
Evaluate your knowledge by spotting errors in the given questions and get a simplified output that can be checked thoroughly with TopperLearning’s CBSE Class 8 Maths solution. Gain a proper insight into the most important questions and go through TopperLearning’s CBSE Class 8 sample papers 2020-21.
NCERT Factorisation Class 8 Videos
NCERT Factorisation Class 8 Revision Notes
NCERT Factorisation Class 8 Most Important Questions
NCERT Factorisation Class 8 MCQ
NCERT Factorisation Class 8 Short Answer Questions
List Of Sub Chapters
Class 8 Maths- Introduction to Factorisation
Class 8 Maths – Factorisation Using Identities
Class 8 Maths – Division of Polynomials
NCERT Solutions for CBSE Class 8 Mathematics Chapter 15 Introduction to Graphs
TopperLearning’s detailed NCERT Solutions for CBSE Class 8 Maths Chapter 15 Introduction to Graphs can help you revise this chapter. Practise with our solutions and understand the correct way to plot graphs based on the given data. Observe how data can be represented on the X-axis and the Y-axis of a graph.
- A bar graph is used to show comparison among categories.
- A pie graph is used to compare parts of a whole.
- A Histogram is a bar graph that shows data in intervals.
- A line graph displays data that changes continuously over periods of time.
- Two perpendicular number lines intersecting at point zero are called coordinate axes.
- The point of intersection of x-axis and y-axis is called origin and is denoted by ‘O’.
- The distance of a point from y-axis is called its x-coordinate and the distance of a point from x-axis is called its y-coordinate.
- The two coordinates x and y taken together for a point P constitutes an ordered pair P(x,y).
- The positions of the coordinates cannot be interchanged. Therefore P(x,y)≠Q(y,x), if x≠y.
- The x- coordinate of every point on y-axis is zero and the y-coordinate of every point on x-axis is zero.
- The x-coordinate of every point on the line parallel to y-axis is constant while y-coordinate of every point on the line parallel to x-axis is constant.
- A line graph which is a whole unbroken line is called a linear graph.
- Two quantities which vary directly can be plotted as a linear graph. Independent variable is generally taken on x axis the dependent variable is taken on y axis.
- Steps to draw a graph:
- Find out the relation between y and x.
- Calculate different values of y corresponding to the values of x.
- Tabulate the results.
- Plot the points.
- oin the points to obtain the graph.
Revise how to construct linear graphs with our Class 8th Maths NCERT solutions. If you have any doubts related to the application of graphs, you can visit the ‘Ask a doubt’ section of our learning platform. Our experts resolve all doubts posted by students through this platform.
Chapter 15 - Introduction to Graphs Exercise Ex. 15.1
Learn how to use a bar graph to represent information and also to answer a question based on the graph. Every solution in TopperLearning’s CBSE Class 8 Maths textbook solutions is explained in detail.
Chapter 15 - Introduction to Graphs Exercise Ex. 15.2
Plot points on a graph and find answers to related to questions. Such questions are often asked in the objective section. Which you can refer to in TopperLearning’s CBSE Class 8 sample papers 2020-21. The CBSE Class 8 Maths solutions assist you when you want to check your methods of solving a problem.
Chapter 15 - Introduction to Graphs Exercise Ex. 15.3
Perform operations and present information on a linear graph and find answers to related questions. TopperLearning’s CBSE Class 8 Maths textbook solutions assist you with ideal solutions.
NCERT Introduction to Graphs Class 8 Videos
NCERT Introduction to Graphs Class 8 Revision Notes
NCERT Introduction to Graphs Class 8 Most Important Questions
NCERT Introduction to Graphs Class 8 MCQ
NCERT Introduction to Graphs Class 8 Short Answer Questions
List Of Sub Chapters
Class 8 Maths- Introduction To Coordinate System
Class 8 Maths – Plotting Linear Graphs
Class 8 Maths – Some Common Linear Graphs
NCERT Solutions for CBSE Class 8 Mathematics Chapter 16 Playing with Numbers
Study your chapter concepts conveniently with NCERT Solutions for CBSE Class 8 Maths Chapter 16 Playing with Numbers. Solve simple problems based on numbers and refer to the answers given by TopperLearning’s subject experts. Learn to use logic while finding answers to number-related games.
- The general form of a 2-digit number ab can be written as:
ab = a × 10 + b × 1,
where a is any whole number from 1 to 9 and b is any whole number from 0 to 9. - The general form of a 3-digit number abc can be written as:
abc = a × 100 + b × 10 + c × 1,
where a is any whole number from 1 to 9, b and c are any whole number from 0 to 9. - The sum of a 2-digit number and the number obtained by reversing the digits is always divisible by 11.
- The difference of a 2-digit number and the number obtained by reversing its digits is always divisible by 9.
- The difference of a 3-digit number and the number obtained by reversing its digits is always divisible by 99.
- Test for divisibility by 2: A number is divisible by 2, if its unit place digit is 0, 2, 4, 6 or 8.
- Test for divisibility by 3: A number is divisible by 3, if the sum of its digits is divisible by 3.
- Test for divisibility by 4: A number is divisible by 4, if the number formed by its digits in tens and units place is divisible by 4.
- Test for divisibility by 5: A number is divisible by 5, if its unit's digit is 0 or 5.
- Test for divisibility by 6: A number is divisible by 6, if it is divisible by both 2 and 3.
- Test for divisibility by 8: A number is divisible by 8, if the number formed by its digits in hundreds, tens and units places is divisible by 8.
- Test for divisibility by 9: A number is divisible by 9, if the sum of its digits is divisible by 9.
- Test for divisibility by 10: A number is divisible by 10, if its unit's digit is zero.
- Test for divisibility by 11: A number is divisible by 11, if the difference of the sum of its digits in odd places and sum of its digits in even places (starting from unit's place) is either 0 or a multiple of 11.
- If two numbers are divisible by a number then their sum and difference are also divisible by that number.
- If a number is divisible by two co-prime numbers then it is divisible by their product also.
Enhance your analytical thinking ability by revising tricky multiplication problems. CBSE Class 8 Maths NCERT textbook solutions are available online 24/7 on our study platform to support you. Use these solutions and other chapter resources for exam preparation, for last-minute revision and to successfully complete your exam paper.
Chapter 16 - Playing with Numbers Exercise Ex. 16.1
As the name of the chapter suggests, this exercise is about understanding patterns of numbers have some fun with them. There are many MCQs from this chapter that can help students practise better. Refer to TopperLearning’s CBSE Class 8 Maths solutions for checking your answers and understanding ways to write stepwise solutions.
Chapter 16 - Playing with Numbers Exercise Ex. 16.2
The fun continues with divisibility tests of numbers and understanding how they are related to other numbers. Check TopperLearning’s CBSE Class 8 Maths solutions for answers and reasons associated with it.
NCERT Playing With Numbers Class 8 Videos
NCERT Playing With Numbers Class 8 Revision Notes
NCERT Playing With Numbers Class 8 Most Important Questions
Benefits of NCERT Solutions Class 8 Maths
Studying Maths takes a lot of practice. Class 8th Maths NCERT solutions helps you to revise concepts such as linear equations, cube roots, square roots, and more. These concepts are the foundation of advanced concepts in higher classes. Also, the knowledge of your Class 8 Maths concepts supports your preparation for competitive exams such as JEE, NEET etc. Our NCERT solutions are available for free and are a reliable reference material to study the concepts as well as the application of concepts as per the most recent NCERT syllabus for Class 8 Maths.
Why should I get TopperLearning NCERT Solutions for Class 8?
TopperLearning’s solutions are utilised by many students so that they don’t to waste time looking for accurate answers online to the exercise questions from the Class 8 Maths textbook. Through TopperLearning’s NCERT Maths textbook solutions for Class 8, you can improve your problem-solving techniques and score good marks. Our Maths experts support your learning by giving more details about the NCERT Class 8 Maths book concepts and on the methods used to solve Maths problems through precise concept notes. If you find a question to be difficult, practise the solution for that problem several times till you have understood it. If you still have any doubts, you can seek support from our Maths experts on our portal.
CBSE Class 8 Maths Frequently Asked Questions
TopperLearning provides free online solutions for exercise questions from your NCERT Class 8 Maths textbook. You can find them under ‘textbook solutions’ in the Class 8 resources section of our study portal.
Solutions for all 16 chapters from the Maths NCERT Class 8 textbook covering topics such as rational numbers, factorisation, practical geometry etc. are available on TopperLearning.
NCERT Solutions for Class 8 Maths are a great resource for revision. However, for scoring high marks, you should practise more Maths problems by attempting CBSE sample paper Class 8 and previous years’ question papers.
First of all, download the latest CBSE NCERT syllabus for Class 8 Maths. Decide whether you want to revise specific chapters or topics from the entire syllabus. Based on your decision, plan your schedule for revising one chapter at a time.
For Maths preparation tips, you can read our blog on how to prepare for CBSE Class 8 Maths here.
No, it was reduced in 2020. The deleted syllabus of CBSE Class 8 is now included in the syllabus and you can find solutions for the deleted syllabus of CBSE Class 8 on TopperLearning.
TopperLearning caters to every need of students and so, the solutions for CBSE Class 8 Science are also available. We also have solutions for CBSE Class 8 English making sure that students are fully prepared for their exams.
Yes. Our academic experts have made sure that the solutions of the CBSE syllabus for Class 8 Maths are apt. The methods used correspond to the ones shown in the NCERT textbooks. TopperLearning’s CBSE syllabus for Class 8 Maths solutions is accepted in all schools. TopperLearning’s CBSE sample paper Class 8 acts as an add on feature and provides you with sample question papers for practice.
CBSE Class 8 syllabus has various subjects and TopperLearning tries its best to cater to students’ needs. Hence, all the NCERT solutions for CBSE Class 8 syllabus including subjects like English, Hindi, and Social Studies are also available.
Hindi is a part of the CBSE Class 8 syllabus and so, we have textbook solutions and sample papers for Hindi in the TopperLearning’s CBSE sample paper Class 8 section.
There are 16 chapters in the NCERT Solutions for Class 8 Maths:
- Rational Numbers
- Linear Equations In One Variable
- Understanding Quadrilaterals
- Practical Geometry
- Data Handling
- Squares And Square Roots
- Cubes And Cube Roots
- Comparing Quantities
- Algebraic Expressions And Identities
- Visualising Solid Shapes
- Mensuration
- Exponents And Powers
- Direct And Inverse Proportions
- Factorisation
- Introduction To Graphs
- Playing With Numbers
Out of these chapters, chapters 2, 3, 8, 13,14, and 16 are considered the most important ones in the Class 8 Maths Solutions book. The CBSE question paper is divided into four sections: A, B, C, and D. These chapters cover most sections.
The following is the mark distribution for each chapter:
- Chapter 2: Linear Equations In One Variable = 10 Marks
- Chapter 3: Understanding Quadrilaterals = 13 Marks
- Chapter 5: Data Handling = 11 Marks
- Chapter 6: Squares And Square Roots = 12 Marks
- Chapter 8: Comparing Quantities = 16 Marks
- Chapter 9: Algebraic Expression And Identities = 12 Marks
- Chapter 11: Mensuration = 15 Marks
- Chapter 14: Factorisation = 12 Marks
- Chapter 15: Introduction To Graphs = 12 Marks
For the upcoming Class 8 Maths examination, you can concentrate more on these chapters in Class 8th Maths NCERT Solutions to achieve good board scores.
You can obtain chapter-by-chapter explanations for Class 8th Maths NCERT Solutions on NCERT's official website. It can be downloaded in pdf format. Aside from that, you can also find it on our official site. To obtain a free copy of the pdf, visit our website and register today.
The answers to questions in Class 8 Maths Solutions are the ideal study tools for students. These CBSE NCERT Solutions for Class 8 Maths 2021-22 help students better understand the ideas taught in the textbook. Solving textbook problems assist students in gaining a deeper understanding of the concept. In addition, the responses in the books aid candidates in resolving the questions rapidly.
The NCERT Solutions for Class 8 Maths list offers explicit and reasonable answers to questions from the NCERT Book for Class 8 Mathematics while conforming to the textbook's objectives. The NCERT Solutions for Class 8 can be used as additional resources and practise tests by candidates. Additionally, as part of their test preparation, students will benefit immensely from studying NCERT textbook practise solutions.
The NCERT Solutions for Class 8 Maths can be downloaded chapter by chapter from their official website. To download all the lessons, follow the steps mentioned below.
- Visit NCERT's official website (https://ncert.nic.in/).
- In the search box, type "Textbooks PDF (I-XII)" and hit "Enter."
- A new page will open.
- Select "Class," "Subject," and "Book Title" as needed on this screen, then click "Go."
- A new page will be displayed. The chapter number of the subject you select will be on the left side, and the front page of its pdf will be on the right side.
- Now select the chapter for which you require Class 8 Maths Solutions. Finally, besides the chapter number, click "Open" to display.
- Now, on the right to the "Print" option, you'll find a download option at the head of the pdf; tap on that, and your document will be downloaded.
On the TopperLearning website, you may also access these Class 8 Maths NCERT pdf solutions. To do so, go to https://www.topperlearning.com and select the class, subject, and chapter number or any other topic you're interested in.