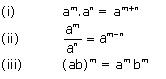Class 9 NCERT Solutions Maths Chapter 1 - Number Systems
Ex. 1.1
Ex. 1.2
Ex. 1.3
Ex. 1.4
Ex. 1.5
Number Systems Exercise Ex. 1.1
Solution 1
Yes zero is a rational number as it can be represented in the 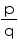 form, where p and q are integers and q
form, where p and q are integers and q 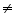 0 as
0 as 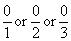 etc.
etc.
Concept Insight: Key idea to answer this question is "every integer is a rational number and zero is a non negative integer". Also 0 can be expressed in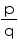 form in various ways as 0 divided by any number is 0. simplest is
form in various ways as 0 divided by any number is 0. simplest is 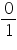 .
.
Concept Insight: Key idea to answer this question is "every integer is a rational number and zero is a non negative integer". Also 0 can be expressed in
Solution 2
There are infinite rational numbers in between 3 and 4.
3 and 4 can be represented as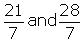 respectively.
respectively.
3 and 4 can be represented as
Now rational numbers between 3 and 4 are
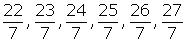
Concept Insight: Since there are infinite number of rational numbers between any two numbers so the answer is not unique here. The trick is to convert the number to equivalent
Solution 3
There are infinite rational numbers between 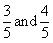
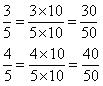
Now rational numbers between are 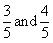
Concept Insight: Since there are infinite number of rational numbers between any two numbers so the answer is not unique here. The trick is to convert the number to equivalent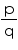 form by multiplying and dividing by the number at least 1 more than the rational numbers required.
form by multiplying and dividing by the number at least 1 more than the rational numbers required.
Alternatively for any two rational numbers a and b,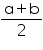 is also a rational number which lies between a and b.
is also a rational number which lies between a and b.
Alternatively for any two rational numbers a and b,
Solution 4
(i) True, since collection of whole numbers contains all natural numbers.
(ii) False, integers include negative of natural numbers as well, which are clearly not whole numbers. For example -1 is an integer but not a whole number.
(iii) False, rational numbers includes fractions and integers as well. For example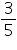 is a rational number but not whole number.
is a rational number but not whole number.
Concept Insight: Key concept involved in this question is the hierarchy of number systems
(ii) False, integers include negative of natural numbers as well, which are clearly not whole numbers. For example -1 is an integer but not a whole number.
(iii) False, rational numbers includes fractions and integers as well. For example
Concept Insight: Key concept involved in this question is the hierarchy of number systems
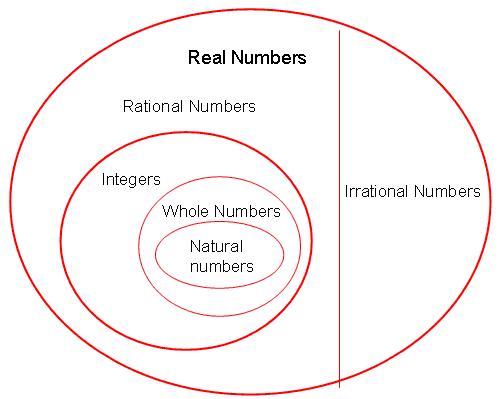
Remember the bigger set consists of the smaller one.
Since Mathematics is an exact science every fact has a proof but in order to negate a statement even one counter example is sufficient.
Since Mathematics is an exact science every fact has a proof but in order to negate a statement even one counter example is sufficient.
Number Systems Exercise Ex. 1.2
Solution 1
(i) True, since real numbers consists of rational and irrational numbers.
(ii) False, Since negative integers cannot be expressed as the square root of any natural number.
(iii) False, real number includes both rational and irrational numbers. So every real number can not be an irrational number.
Concept Insight: Mentioning the reasons is important in this problem. Real Numbers consists of rational and irrational numbers and not vice versa. Every real number corresponds to a point on number line and vice versa.
Recall real number includes negative numbers also. Square root of negative numbers is not defined.
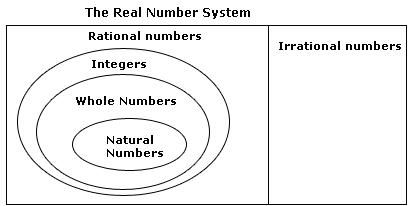
(ii) False, Since negative integers cannot be expressed as the square root of any natural number.
(iii) False, real number includes both rational and irrational numbers. So every real number can not be an irrational number.
Concept Insight: Mentioning the reasons is important in this problem. Real Numbers consists of rational and irrational numbers and not vice versa. Every real number corresponds to a point on number line and vice versa.
Recall real number includes negative numbers also. Square root of negative numbers is not defined.

Solution 2
Square roots of all square numbers are rational.
For example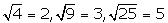
For example
Thus the square roots of all positive integers are not irrational
Concept Insight: In general only the square root of a prime number is irrational.
Therefore square root of perfect square numbers are rational.
Solution 3
Using Pythagoras Theorem: 5=22+12
Taking positive square root we get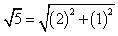
Taking positive square root we get
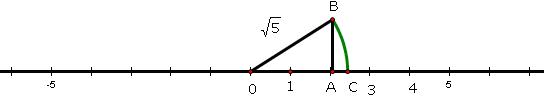
1. Mark a point 'A' representing 2 units on number line.
2. Now construct AB of unit length perpendicular to OA. Join OB
3. Now taking O as centre and OB as radius draw an arc, intersecting number line at point C.
4. Point C represents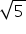 on number line. [length (OB) = length (OC)]
on number line. [length (OB) = length (OC)]
2. Now construct AB of unit length perpendicular to OA. Join OB
3. Now taking O as centre and OB as radius draw an arc, intersecting number line at point C.
4. Point C represents
Concept Insight: For a positive integer n, 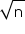 can be located on number line , if
can be located on number line , if 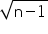 is located using Pythagoras Theorem . If is a perfect square then this method is useful.
is located using Pythagoras Theorem . If is a perfect square then this method is useful.
To represent the irrational number 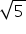 key idea is to use Pythagoras theorem and create a length of
key idea is to use Pythagoras theorem and create a length of 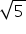 units by constructing a right triangle of base and perpendicular of length 2 and 1 units.
units by constructing a right triangle of base and perpendicular of length 2 and 1 units.
Number Systems Exercise Ex. 1.3
Solution 1
(i) 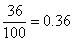
terminating
(ii)
(ii)
non terminating repeating
(iii)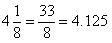
(iii)
Terminating
(iv)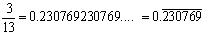
(iv)
non terminating repeating
(v)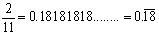
(v)
non terminating repeating decimal
(vi)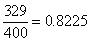
(vi)
Terminating decimal
Concept Insight: The decimal expansion of a rational number is either terminating or non terminating recurring.
Decimal expansion terminates in case the prime factors of denominator includes 2 or 5 only.
Concept Insight: The decimal expansion of a rational number is either terminating or non terminating recurring.
Decimal expansion terminates in case the prime factors of denominator includes 2 or 5 only.
Solution 2
Yes it can be done as follows:
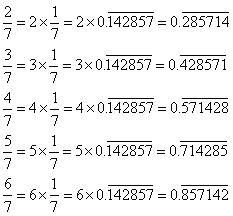
Concept Insight: Multiples of the given decimal expansion can be obtained by simple multiplication with the given constant. Cross check the answer by performing long division.
Solution 3
(i) 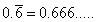
Let x = 0.666 ... (i)
Multiplying by 10 we get
10x = 6.666 ... (ii)
(ii) - (i) gives
9x = 6
Or x =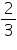
(ii)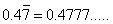
Let x = 0.4777 ... (i)
10x = 4.777 ...
100x = 47.777 ... (ii)
(ii) - (i) gives
99 x = 43
Multiplying by 10 we get
10x = 6.666 ... (ii)
(ii) - (i) gives
9x = 6
Or x =
(ii)
Let x = 0.4777 ... (i)
10x = 4.777 ...
100x = 47.777 ... (ii)
(ii) - (i) gives
99 x = 43
x = 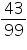
(iii)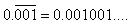
(iii)
Let x = 0.001001 ...(i)
1000x = 1.001001 ...(ii)
(ii) - (i) gives
999x = 1
x =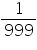
Concept Insight: The key idea to express a recurring decimal in the p/q form is to multiply the number by the 10n where n = number of digits repeating.
This is done to make the repeating block a whole number part of the decimal. By subtracting the two expressions x can be expressed in the P/q form
x =
Concept Insight: The key idea to express a recurring decimal in the p/q form is to multiply the number by the 10n where n = number of digits repeating.
This is done to make the repeating block a whole number part of the decimal. By subtracting the two expressions x can be expressed in the P/q form
Solution 4
Let x = 0.9999 .. .. ..(i)
10x = 9.9999 ... ...(ii)
(ii) - (i) gives
9x = 9
x = 1
10x = 9.9999 ... ...(ii)
(ii) - (i) gives
9x = 9
x = 1
Concept Insight: .9999999 ..... is nothing but 1 when expressed in p/q form.
Solution 5
Expressing 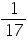 in the decimal form we
in the decimal form we
There are 16 digits in repeating block of decimal expansion of
Concept Insight: Maximum number of digits that can repeat will be 1 less than the prime number in denominator.
Solution 6
Terminating decimal expansion will come when denominator q of rational number 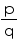 , is either of 2, 4, 5, 8, 10, and so on ... ...
, is either of 2, 4, 5, 8, 10, and so on ... ...
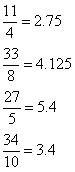
Terminating decimal may be obtained in the situation where prime factorisation of the denominator of the given fractions are having power of 2 only or 5 only or both.
Concept Insight: A rational number in its simplest form will terminate only when prime factors of its denominator consists of 2 or 5 only.
Solution 7
3 numbers whose decimal expansion is non terminating non recurring are ... ... ,
0.505005000051509 ... ... ...
0.72012009200011500007200000 ... ... ...
7.03124509761202 ... ... ... ... ... ...
Concept Insight: Recall that a non terminating non recurring decimal is an irrational number. Answer to such questions is not unique.
0.505005000051509 ... ... ...
0.72012009200011500007200000 ... ... ...
7.03124509761202 ... ... ... ... ... ...
Concept Insight: Recall that a non terminating non recurring decimal is an irrational number. Answer to such questions is not unique.
Solution 8
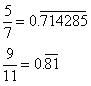
3 irrational numbers are -
0.73073007300073000073 ... ... ...
0.73073007300073000073 ... ... ...
0.75075007500075000075 ... ... ...
0.79079007900079000079 ... ... ...
0.79079007900079000079 ... ... ...
Concept Insight: There is infinite number of rational and irrational numbers between any two rational numbers. Convert the number into its decimal form to find irrationals between them.
Alternatively following result can be used to answer
Irrational number between two numbers x and y

Solution 9
(i) 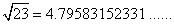
As decimal expansion of this number is non-terminating non recurring. So it is an irrational number.
(ii) 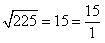
Rational number as it can be represented in 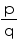 form.
form.
(iii) 0.3796
As decimal expansion of this number is terminating, so it is a rational number.
As decimal expansion of this number is terminating, so it is a rational number.
(iv) 
As decimal expansion of this number is non terminating recurring so it is a rational number.
(v) 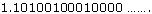
As decimal expansion of this number is non terminating non repeating so it is an irrational number.
Concept Insight: A number is rational if its decimal expansion is either terminating or non terminating but recurring. A number which cannot be expressed in p/q form is irrational. Square root of prime numbers is always irrational.
Number Systems Exercise Ex. 1.4
Solution 1
(i) 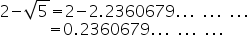
As decimal expansion of this expression is non terminating non recurring, so it is an irrational number.
(ii) 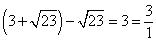
It can be represented in 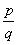 form so it is a rational number.
form so it is a rational number.
(iii) 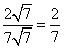
As it can be represented in 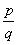 form, so it is a rational number.
form, so it is a rational number.
(iv) 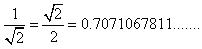
As decimal expansion of this expression is non terminating non recurring, so it is an irrational number.
(v) 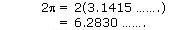
As decimal expansion is non terminating non recurring, so it is an irrational number.
Concept Insight: Do the simplifications as indicated and see whether the number is terminating, non terminating recurring or neither terminating nor repeating. Remember Sum/difference/Product of a rational and irrational number may or may not be irrational.
Solution 2
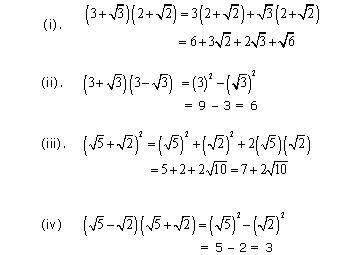
Concept Insight: Apply the algebraic identities (a+b)2, (a-b)2,(a+b)(a-b) etc to simplify the given expressions.
Equivalent Identities used here are
Equivalent Identities used here are
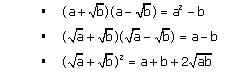
Solution 3
There is no contradiction. Since 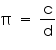 here circumference or diameter are not given to be integers . When we measure a length with scale or any other instrument, we only get an approximate rational value. We never get an exact value. c or d may be irrational. So, the fraction
here circumference or diameter are not given to be integers . When we measure a length with scale or any other instrument, we only get an approximate rational value. We never get an exact value. c or d may be irrational. So, the fraction 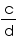 is irrational. Therefore,
is irrational. Therefore, 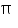 is irrational.
is irrational.
Concept Insight: A rational number is the number of the form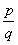 where p and q are
where p and q are
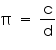 here circumference or diameter are not given to be integers . When we measure a length with scale or any other instrument, we only get an approximate rational value. We never get an exact value. c or d may be irrational. So, the fraction
here circumference or diameter are not given to be integers . When we measure a length with scale or any other instrument, we only get an approximate rational value. We never get an exact value. c or d may be irrational. So, the fraction Concept Insight: A rational number is the number of the form
integers. In 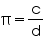 c and d are not integers. Also remember that no measurement is exact.
c and d are not integers. Also remember that no measurement is exact.
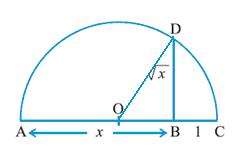
Solution 4
(i) Mark a line segment OB = 9.3 on number line.
(ii) Take BC of 1 unit.
(iii) Find mid point D of OC and draw a semicircle on OC while taking D as its centre.
(iv) Draw a perpendicular to line OC passing through point B. Let it intersect semicircle at E. Length of perpendicular BE = 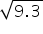 .
.
(v) Taking B as centre and BE as radius draw an arc intersecting number line at F. BF is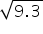 i.e point F represents
i.e point F represents 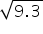 on number line
on number line
(v) Taking B as centre and BE as radius draw an arc intersecting number line at F. BF is
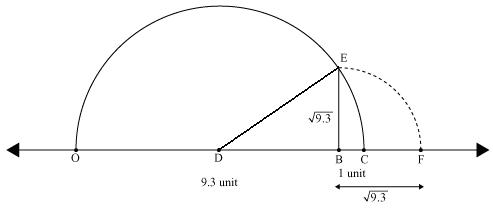
Verification: In  EDB
EDB
ED2=EB2+DB2 Using Pythagoras theorem
ED2=EB2+DB2 Using Pythagoras theorem
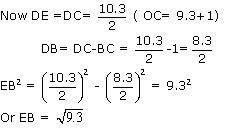
Concept Insight: This method based on the application of Pythagoras theorem can be used to represent root of any rational number on the number line.
The key idea to represent 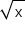 is to create a length of
is to create a length of 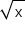 units.
units.
In ODB
ODB
In
DB = 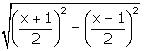
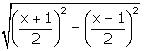
Solution 5
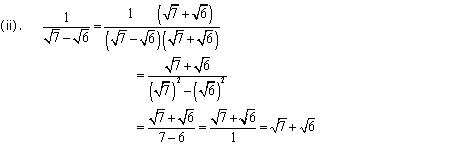
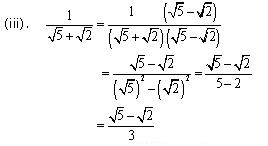
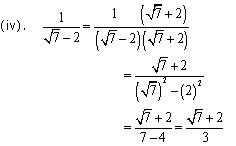
Concept Insight: Rationalisation of denominator means converting the irrational denominator to rational i.e . removing the radical sign from denominator.A number of the form 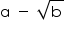 can be converted to rational form by multiplying with its conjugate. Remember the algebraic identities
can be converted to rational form by multiplying with its conjugate. Remember the algebraic identities
Number Systems Exercise Ex. 1.5
Solution 1
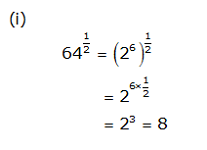
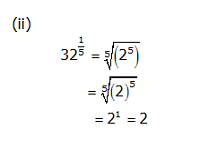
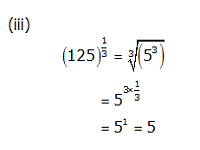
Concept Insight: Express the number in exponent notation and use the rule 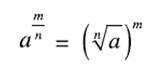 Exponent m must be such that it is divisible by n.
Exponent m must be such that it is divisible by n.
Solution 2
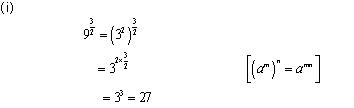
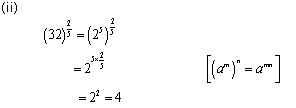
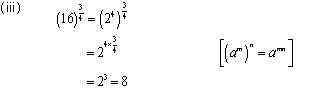
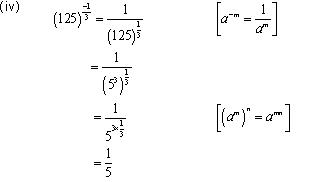
Concept Insight: Express the number in exponent notation and use the rule of exponents.
Solution 3
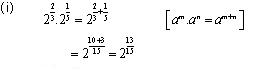
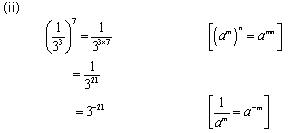
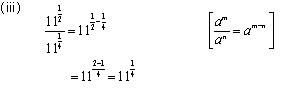
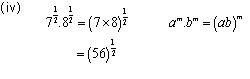
Concept Insight: Use the rule of exponents